엘로 레이팅 시스템(Elo rating system)은 특정 분야의 게임에서 선수들의 실력을 측정하는 대표적인 지표이다. 헝가리 출신 미국의 물리학자인 아르파드 엘로(Arpad Elo)가 고안하였다. 가끔 'ELO'를 이름의 이니셜로 오해하는 사람들이 있어서 그런지 "이엘오"라 부르기도 하는데 성씨 그대로 "엘로"가 맞다.
이 시스템은 본래 체스에서 쓰였으며, 후에 공식 또는 비공식으로 이러한 점수 산출 방식을 여러 게임에서 쓰이고 있다. 오델로도 마찬가지로 레이팅 시스템을 마련할 수 있고, 실제로 한국 오델로 협회에서도 이 방식을 써서 "오델로 기사 순위" 목록을 홈페이지에 게시 및 업데이트를 하고 있다. (세계 오델로 연맹에서는 다른 방식을 쓴다) 오델로 퀘스트나 리버시 달인도 세부 방식은 다르지만 자체 레이팅을 셈한다.
어떤 선수의 실력을 '수치'로 나타낸다면 어떻게 접근해야 할까? 자세한 셈법은 꽤 복잡하지만 여기서는 레이팅 계산의 기본 원리 위주로 소개하겠다. (수식 주의)
◆ 기대 승수 산출하기 ◇
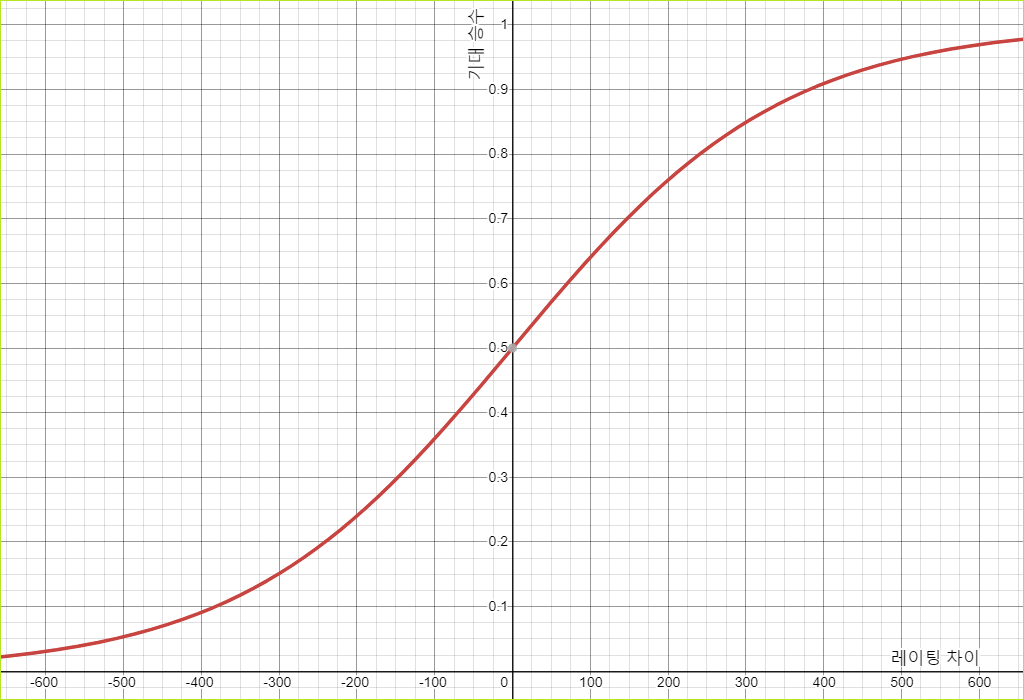
먼저 오델로나 체스와 같이 1:1로 붙어서 승패를 가리는 경기라는 기본 전제를 깔아둔다. 당연한 이야기지만 레이팅 값이 높을 수록 실력이 높고, 그에 따라 기대 승수가 높아진다. 여기서 '승률'이라 하지 않고 '기대 승수'라고 부르는 이유는 아래 섹션에서 확인할 수 있다.
좀 더 구체적으로 레이팅과 기대 승수 사이의 관계를 아래와 같이 설정한다.
▷ 한 판 대국 시 두 선수의 기대 승수의 합은 언제나 1이다.
▷ 두 선수의 레이팅 값이 같으면 기대 승수는 각각 0.5로 같다. 즉 승리 확률과 패배 확률이 같다.
▷ 기대 승수는 두 선수의 레이팅의 차로만 결정한다. 다시 말해 레이팅이 각각 (1200, 1300)이든 (1600, 1700)이든 (2100, 2200)이든 상관 없이 차이가 100점으로 같다면 기대 승수의 분배는 언제나 똑같다.
▷ 두 선수의 레이팅의 차가 400점이면 높은 쪽의 기대 승수는 낮은 쪽의 10배로 정한다. (즉 높은 쪽 10/11, 낮은 쪽 1/11)
위 설정 중 네 번째 규칙은 레이팅 점수의 스케일을 정하는 척도로, 아래 계산에 사용할 것이다. 그렇다면 레이팅의 차가 0점도 400점도 아닌 일반적인 경우라면 기대 승수를 어떻게 정해야 할까?
§ 실력의 대소 비교
여기 선수마다 대응하는 확률 변수를 불러오자. 이 확률 변수는 어떤 판에서 발휘할 해당 선수의 '기량'을 나타낸다. 특정 판에서 두 선수의 기량을 비교하고, 더 높게 나타나는 쪽이 승리한다고 하자. 이때 몇 점 차로 승리하는 지는 관심의 대상이 아니다. 단지 승리를 1승, 패배를 0승으로 처리하고, 무승부는 고려하지 않는다. (오델로 대회에서 무승부가 나오면 0.5승으로 간주한다)
우리는 확률 변수의 구체적인 값이나 분포는 모르고 '대소 비교'에만 초점을 둘 것이다. 이제 선수 A, B, C의 레이팅을 각각 \(R_A, R_B, R_C\)라 하고, 기량을 나타내는 확률 변수를 \(X_A, X_B, X_C\)라 하자.
선수 A가 B를 이길 확률은 \(P(X_A>X_B)\)라 쓸 수 있다. 반대로 B가 A를 이길 확률은 \(P(X_A<X_B)\)가 되고, 두 값을 합하면 1이 된다. (편의상 등호 조건은 생략)
그렇다면 여기서 질문: 우리는 세 선수 중 A와 B, B와 C 사이의 승패 확률을 각각 알고 있다. 그러면 A와 C가 붙을 때 승패 확률은 얼마가 될까? 이 부분은 아래와 같이 네 가지 경우로 나누어서 생각한다.
① \(X_A>X_B \text{ and } X_B>X_C\) ― \(X_A>X_C\), 즉 A는 C를 이긴다. 이 경우가 일어날 확률은 \(P(X_A>X_B) \cdot P(X_B>X_C)\)라 쓸 수 있다.
② \(X_A>X_B \text{ and } X_B<X_C\) ― \(X_A\)와 \(X_C\) 사이의 대소는 모른다. 판단 유보.
③ \(X_A<X_B \text{ and } X_B>X_C\) ― \(X_A\)와 \(X_C\) 사이의 대소는 모른다. 판단 유보.
④ \(X_A<X_B \text{ and } X_B<X_C\) ― \(X_A<X_C\), 즉 A는 C에게 진다. 이 경우가 일어날 확률은 \(P(X_A>X_B) \cdot P(X_B>X_C)\)라 쓸 수 있다.
①④의 경우는 A와 C 사이의 기량 비교가 명확하기에 승패 여부를 확실하게 말할 수 있다. 하지만 문제는 ②③이다. 부등호가 엇갈리는 경우에는 A와 C 중 누가 이기는지 확신할 수 없다. 사실 확률 변수의 분포 함수를 알고 있다면 승패 확률을 어떻게 계산을 해볼 수는 있겠지만, 실제 대국에서 각 선수가 각 판에서 기량을 얼만큼 발휘하는 지 정량적으로 측정할 수 있는가? 실제로는 그렇지 못하다.
앞서 언급했듯이 우리는 단순 대소 비교를 중심으로 접근하고 있다. 이 경우 "불명확한 정보는 과감하게 솎아내기"로 한다. 다시 말해 승리 확률과 패배 확률의 비는 정보가 명확한 ①④의 경우만으로 셈할 것이며, ②③ 역시 같은 비율로 승패 확률을 내포한다고 가정할 것이다.
수식으로 표현하면 이렇다: 분자는 A가 C를 이길 때, 분모는 반대로 질 때를 나타낸다.
\[ \frac{P(X_A>X_C)}{P(X_A<X_C)} = \frac{P(X_A>X_B) \cdot P(X_B>X_C)}{P(X_A<X_B) \cdot P(X_B<X_C)}\]
§ 승패 비율 함수
좀 복잡해 보이지만 아래 승패 비율 함수를 도입해서 간단하게 써보자.
\[Q(A|B) = \frac{P(X_A>X_B)}{P(X_A<X_B)}\]
이렇게 정의하면 \(Q(A|B) \cdot Q(B|A) = 1\)이 성립함을 알 수 있다.
그러면 위 식은 \(Q(A|C) = Q(A|B) \cdot Q(B|C)\)와 같이 써진다. 그리고 이 식을 변형해서 \(Q(A|B) = Q(A|C) \cdot Q(C|A)\) 내지는 \(Q(B|C) = Q(B|A) \cdot Q(A|C)\)와 같이 쓸 수도 있다.
한편 A와 B가 붙을 때 A의 기대 승수를 \(P(X_A>X_B) = E(A|B)\) 라 하면 \(P(X_A<X_B) = E(B|A) = 1-E(A|B)\)이므로, 승패 비율 함수와의 관계는 아래와 같다.
\[Q(A|B) = \frac{E(A|B)}{1-E(A|B)}, E(A|B) = \frac{Q(A|B)}{Q(A|B)+1} = \frac{1}{1+Q(B|A)}\]
§ 공식 세우기
이번에는 승패 비율 함수의 특징을 좀 더 살펴본다. 앞서 정해놓은 가정 중 "레이팅의 차로 기대 승수를 결정한다"는 조건에 주목하자. 이 말은 곧 승패 비율 함수도 레이팅의 차로 결정된다는 의미가 된다.
그러면 \(Q(A|B) = Q(R_A-R_B)\)와 같이 변수가 하나인 함수로 다시 표현할 수 있다. 그리고 위 관계식은 \(Q(R_A-R_C) = Q(R_A-R_B) \cdot Q(R_B-R_C)\)와 같이 써진다.
이때 \(R_A-R_B = x, R_B-R_C = y\)로 치환하면 \(R_A-R_C = x+y\)이므로, \(Q(x+y)=Q(x)Q(y)\)가 성립한다. 특히 \(y\) 대신 \(-x\)를 대입하면 \(Q(x)Q(-x)=Q(0)=1\)임을 알 수 있다.
오호라! 이런 형태의 함수는 수학에서 종종 등장한다. 다름 아닌 지수 함수. 따라서 \(Q(x) = a^x\)의 꼴로 나타낼 수 있고, 이제 상수 \(a\)의 값을 결정할 차례다. 앞서 세운 가정 중 마지막 조건을 다시 가져오자. 레이팅이 400점 앞설 때, 승리 확률이 패배 확률의 10배라고 가정하였다. 그러면 승패 비율 함수로 쓰면 \(Q(400)=10\)이다. 이 조건을 만족하는 \(a\)의 값은 \(a=10^{(1/400)}\).
드디어 우리는 승패 비율 함수를 찾았다.
\[Q(x) = 10^{\frac{x}{400}}, Q(A|B) = 10^{\frac{R_A-R_B}{400}}\]
또한 A와 B가 서로 붙을 때, 각자의 기대 승수는 아래와 같으며, 두 기댓값을 합하면 1이 됨을 확인할 수 있다.
\[E(A|B) = \frac{1}{1+10^{\frac{R_B-R_A}{400}}}, E(B|A) = \frac{1}{1+10^{\frac{R_A-R_B}{400}}}\]
◆ 대회 적용과 레이팅 증감 ◇
이제 실전 대회에 들어가보자. 레이팅 시스템을 구성하면서 기대 승수를 분석하는 이유는 대회에서 나오는 실제 승수와 비교하기 위함이다. 레이팅은 기본적으로 승리 시 올라가고 패배 시에는 내려간다. 그리고 레이팅이 높은 상대를 이길수록 더 크게 올라가고, 반대로 레이팅이 낮은 상대에게 지면 크게 떨어지게 설계한다.
실전에서 여러 판을 진행하고 각 선수 별로 승점(=승수)을 합산하자. 이때 승리는 1pt, 패배는 0pt, 무승부는 0.5pt이다. 그리고 각 선수 별로 각 판의 상대와 만날 때마다 레이팅을 대조하고, 그에 따라 기대 승수도 똑같이 합산한다. 판이 끝나고, 각 선수마다 누적된 기대 승수와 실제 승수를 산출할 수 있다. 이 두 지표가 레이팅의 변화를 결정한다.
▷ 실제 승수가 기대 승수보다 많으면 → "이 선수는 기대보다 좋은 성적을 냈으니 레이팅을 올리자"
▷ 실제 승수가 기대 승수에 못 미치면 → "이 선수는 기대만큼의 성적을 올리지 못했으니 레이팅을 내리자"
대회가 끝나고 한 선수의 레이팅 증감은 {(실제 승수) - (기대 승수)}에 어떤 상수를 곱해서 계산한다. 한국 오델로 협회에서는 32로 잡는다.
§ 적용 예
어떤 대회에서 선수 A, B, C, D가 6라운드, 즉 풀 리그를 두 바퀴 돌았다. 그리고 각 판마다 아래와 같이 판가름 났다고 하자.
●1라운드: A vs B -- A 승, C vs D -- 무승부
○2라운드: C vs A -- A 승, D vs B -- B 승
●3라운드: A vs D -- D 승, B vs C -- C 승
○4라운드: B vs A -- A 승, D vs C -- C 승
●5라운드: A vs C -- A 승, C vs D -- D 승
○6라운드: D vs A -- D 승, C vs B -- B 승
그러면 각 선수의 승점은 ABCD 순으로 4, 2, 2.5, 3.5pt가 된다.
한편 대회 전 레이팅은 각각 1934, 1685, 1678, 1596이었다고 하자. 각 매치마다 레이팅을 대조하고 기대 승수와 레이팅 증감을 아래 표와 같이 작성할 수 있다.
| 플레이어, 대회 전 레이팅 |
라운드 | 레이팅 증감 (승수 차*32) |
대회 후 레이팅 | ||||||
| 대회 승수 | 1 | 2 | 3 | 4 | 5 | 6 | 기대 승수 합 | 승수 차 | |
| A, 1934 | 상대 | B | C | D | B | C | D | -31.74 | 1902.26 |
| 4pt | 기대 승수 | 0.807 | 0.814 | 0.875 | 0.807 | 0.814 | 0.875 | 4.992 | -0.992 |
| B, 1685 | 상대 | A | D | C | A | D | C | -20.99 | 1664.01 |
| 2pt | 기대 승수 | 0.193 | 0.625 | 0.510 | 0.193 | 0.625 | 0.510 | 2.656 | -0.656 |
| C, 1678 | 상대 | D | A | B | D | A | B | -2.70 | 1675.30 |
| 2.5pt | 기대 승수 | 0.616 | 0.186 | 0.490 | 0.616 | 0.186 | 0.490 | 2.584 | -0.084 |
| D, 1596 | 상대 | C | B | A | C | B | A | +55.44 | 1651.44 |
| 3.5pt | 기대 승수 | 0.384 | 0.375 | 0.125 | 0.384 | 0.375 | 0.125 | 1.767 | +1.733 |
따라서 대회 후 레이팅은 각각 1902, 1664, 1675, 1651이 된다. 물론 소수점 아래를 어떻게 처리하느냐에 따라 ±1 오차가 날 수는 있다. 위 결과에서 대회 전 레이팅이 가장 낮은 D가 유일하게 상승하였고, 가장 높은 A는 리그에서 1위를 했음에도 기대 승수에 못 미쳐서 레이팅이 오히려 내려갔다. C의 경우 실제 승수와 기대 승수의 차가 작아서 레이팅 변동도 작다.
참고: 기대 승수는 어떤 대회에서 특정 선수가 거둘 수 있는 승점의 기댓값이다. 이는 전체 전적에 대한 승수 비율인 승률과는 의미상 차이가 있다.
첨언하자면 레이팅 증감을 계산할 때에는 두 가지 방법이 있다.
▷ 대회 전 레이팅을 기준으로 하는 방법: 같은 대회 내에서 선수의 기량이 정해져 있다고 가정한다. 실제 승수와 기대 승수를 따로 한꺼번에 합산하며, 위 예시는 이 기준을 적용했다.
▷ 매 라운드마다 레이팅을 갱신하는 방법: 이 경우 기준 레이팅이 계속 바뀐다. 승수가 일정할 때, 전반전에 지고 후반전에 이기는 꼴이면 레이팅 상승이 두드러진다.
한국 오델로 협회에서는 오프라인 대회 첫 참가자를 기본 1600점부터 출발한다. 그리고 오델로 프로기사 순위 표에는 안 나와 있지만 국내 대회에 참가한 이력이 한 번이라도 있다면 아마단급이나 외국인들도 협회 자체 레이팅이 기록되어 있다. 단지 필자 본인은 그 정보에 접근할 권한이 없을 뿐이다.
'대회 관련 정보' 카테고리의 다른 글
| WOF 온라인 대회 치팅 방지 정책 (0) | 2021.08.16 |
|---|---|
| 오프라인 대회 참가자들을 위한 팁 모음 (0) | 2021.08.12 |
| MBS 분석 (0) | 2020.05.16 |
| 오델로 대회와 스위스 방식 (0) | 2020.05.12 |
| 한국 오델로 협회 대회 규정 (0) | 2019.12.02 |
